distribute n balls m boxes Take $3$ balls and $2$ buckets: your formula gives $\frac43$ ways to distribute the balls. $\endgroup$ – Villa Roofing and Sheet Metal is a General Contractor, Specialty Contractor that serves the Vancouver, BC area and specializes in Roofing. How are these metrics calculated? Automate workflows, standardize documents, enable visibility, and track budgets in real time with Procore Project Management.
0 · probability n balls m boxes
1 · n balls and m boxes
2 · math 210 distribution balls
3 · how to distribute n boxes
4 · how to distribute k balls into boxes
5 · how many balls in a box
6 · distribution of balls into boxes pdf
7 · distributing balls to boxes
DTECH 2 Way Powered VGA Splitter Amplifier Box High Resolution 1080p .
Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. .Take $ balls and $ buckets: your formula gives $\frac43$ ways to .Number of ways to distribute five red balls and five blues balls into 3 distinct boxes .Distributing k distinguishable balls into n distinguishable boxes, with exclusion, corresponds to forming a permutation of size k, taken from a set of size n. Therefore, there are P(n, k) n k n n .
Take $ balls and $ buckets: your formula gives $\frac43$ ways to distribute the balls. $\endgroup$ –Number of ways to distribute five red balls and five blues balls into 3 distinct boxes with no empty boxes allowed
The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves m balls and n boxes (or .
sheet metal roller cutter
The number of ways to place n balls into m boxes can be calculated using the formula n^m (n raised to the power of m). This formula assumes that each ball can be placed . Find the number of ways that n balls can be distributed among m boxes such that exactly k boxes each contain exactly ##\ell## balls. Define ##N_{\ell}(n, m)## to be the .Suppose there are n n identical objects to be distributed among r r distinct bins. This can be done in precisely \binom {n+r-1} {r-1} (r−1n+r−1) ways. Modeled as stars and bars, there are n n stars in a line and r-1 r −1 bars that divide them . The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, .
Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. For example, one way is that all $N$ balls land in one box.Distributing k distinguishable balls into n distinguishable boxes, with exclusion, corresponds to forming a permutation of size k, taken from a set of size n. Therefore, there are P(n, k) n k n n distribute k distinguishable balls into n distinguishable boxes, with exclusion.Take $ balls and $ buckets: your formula gives $\frac43$ ways to distribute the balls. $\endgroup$ –Number of ways to distribute five red balls and five blues balls into 3 distinct boxes with no empty boxes allowed
The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.
The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves m balls and n boxes (or "bins"). Each time, a single ball is placed into one of the bins.
The number of ways to place n balls into m boxes can be calculated using the formula n^m (n raised to the power of m). This formula assumes that each ball can be placed in any of the m boxes, and that order does not matter. Find the number of ways that n balls can be distributed among m boxes such that exactly k boxes each contain exactly ##\ell## balls. Define ##N_{\ell}(n, m)## to be the number of ways to distribute n balls in m boxes such that NONE of them contain exactly ##\ell##. We can explicitly count these ways with the following formula:Suppose there are n n identical objects to be distributed among r r distinct bins. This can be done in precisely \binom {n+r-1} {r-1} (r−1n+r−1) ways. Modeled as stars and bars, there are n n stars in a line and r-1 r −1 bars that divide them into r r distinct groups. The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, and 1 - in this case M=4 and N=3).
Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. For example, one way is that all $N$ balls land in one box.
Distributing k distinguishable balls into n distinguishable boxes, with exclusion, corresponds to forming a permutation of size k, taken from a set of size n. Therefore, there are P(n, k) n k n n distribute k distinguishable balls into n distinguishable boxes, with exclusion.Take $ balls and $ buckets: your formula gives $\frac43$ ways to distribute the balls. $\endgroup$ –Number of ways to distribute five red balls and five blues balls into 3 distinct boxes with no empty boxes allowed
The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.
The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves m balls and n boxes (or "bins"). Each time, a single ball is placed into one of the bins. The number of ways to place n balls into m boxes can be calculated using the formula n^m (n raised to the power of m). This formula assumes that each ball can be placed in any of the m boxes, and that order does not matter.
Find the number of ways that n balls can be distributed among m boxes such that exactly k boxes each contain exactly ##\ell## balls. Define ##N_{\ell}(n, m)## to be the number of ways to distribute n balls in m boxes such that NONE of them contain exactly ##\ell##. We can explicitly count these ways with the following formula:Suppose there are n n identical objects to be distributed among r r distinct bins. This can be done in precisely \binom {n+r-1} {r-1} (r−1n+r−1) ways. Modeled as stars and bars, there are n n stars in a line and r-1 r −1 bars that divide them into r r distinct groups.
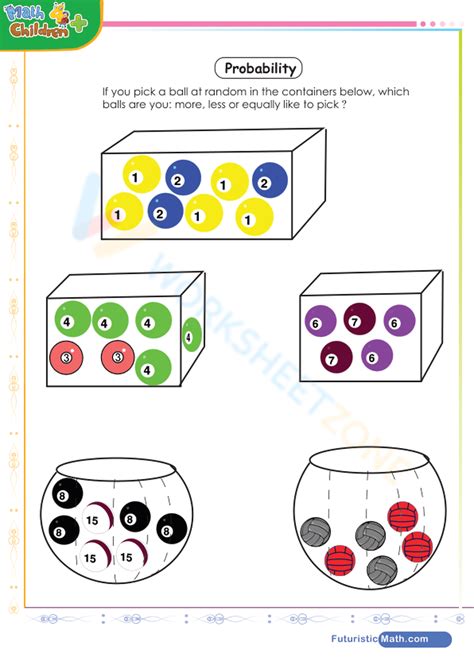
probability n balls m boxes

Smart Vietnam is a leading sheet metal fabricator in Vietnam, providing a range of services to customers across different industries. Our services include engineering support, laser cutting, punching, forming, folding & bending, welding, powder coating and liquid paint, metal finishing, Hardware & assembly, and quality control & inspection. We work with a variety of materials, .
distribute n balls m boxes|math 210 distribution balls