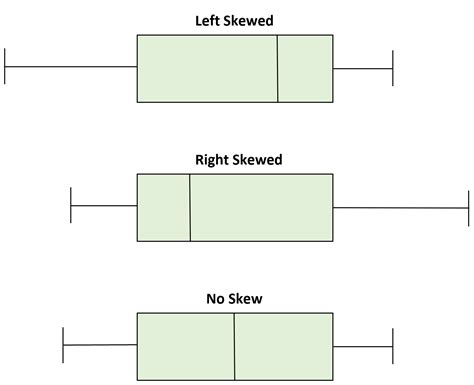
how to guess distribution based on box plots A boxplot, also known as a box-and-whisker plot, is a fantastic tool for visualizing the distribution, spread, and variability of your data. Think of it as a quick summary of your data’s story—it . Drive mounting screws (included with Verkada device) directly into the pilot holes using the relevant hole pattern (A - E) of the junction box. Separate wall anchors may be required. Feed Ethernet cable through the center of the junction box before fully securing it .
0 · symmetrical box plot
1 · reading box plot sizes
2 · how to find box distribution
3 · box plots explained
4 · box plot calculation
5 · box and whisker plot probability
6 · box and whisker plot example
7 · box and whisker plot calculator
The minimalist silhouette of this planter box provides compelling contrast with the wild lines of outdoor plants. Handmade from galvanized steel with a powder-coated finish, it stands up to frost, sun, and storms, while its foam insulation protects your garden from extreme temps.
A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset. A box plot displays a ton of . Ask Question. Asked 7 years, 8 months ago. Modified 2 years, 11 months ago. Viewed 23k times. 12. Suppose we're looking at this box-and-whisker plot: Between Thursday and Friday, I think most would agree there .
A boxplot, also known as a box-and-whisker plot, is a fantastic tool for visualizing the distribution, spread, and variability of your data. Think of it as a quick summary of your data’s story—it .A box plot, also known as a box-and-whisker plot, is a standardized way of displaying the distribution of data based on a five-number summary: minimum, first quartile (Q1), median, third quartile (Q3), and maximum. The box part of . A box plot is a standardized way of displaying the distribution of a dataset based on a five-number summary: minimum, first quartile (Q1), median, third quartile (Q3), and maximum. It. Box plots are useful for identifying outliers and for comparing distributions. We will explain box plots with the help of data from an in-class experiment. As part of the "Stroop Interference Case Study," students in .
symmetrical box plot
The distribution of data is shown through the positions of the median and the quartiles. From this, the spread and skew of the data can also be seen. Side-by-side box plots allow for two or more data sets to be compared in a graphical .
old work metal outlet box
Techniques for visualizing data spread. Crafting and analyzing your box plot masterpiece. Numbers have stories; give them voice with box plots. Table of Contents. What Is A Box Plot? Box Plot Example. When To Use A .A boxplot is a standardized way of displaying the distribution of data based on its five-number summary (“minimum”, first quartile [Q1], median, third quartile [Q3] and “maximum”). Boxplots can tell you about your outliers and their values, if .
I have tried create box plot with jitter but cant explain it very clearly. Could some one help? . (or another values between 0 and 1) and obtain a transparency that can be also used a rough way to measure distribution . Related post: Understanding the Weibull Distribution. Using Probability Plots to Identify the Distribution of Your Data. Probability plots might be the best way to determine whether your data follow a particular distribution. . How do we read statistics from a cumulative frequency graph? Quartiles and percentiles can be read from a cumulative frequency graph. The median, Q 2 is read from the y – axis scale at the th value The lower quartile, .
btw I love having a Visual look at the variance/distribution/pattern before embarking on any statistical/modelling analysis. If I'm building something, like an econometric model, and don't want to run all 60 of my 'candidate' variables through SPSS (or similar) and get that horrible cross-table!!.Having a quick Visual look first really helps . In a box plot, it is represented by the width of the box, which ranges from the first quartile (Q1) to the third quartile (Q3) Often we create multiple box plots on one plot to compare the distribution of several datasets at once. The following example shows how to compare the variability between several box plots in practice.Lets say you have a 5 number summary of 5,10,15,20,25 with n=100. The two most extremes of the first quartiles is that all 25 data points equal 5 or that one equals 5 and that the other 24 all equal 10.Use a box plot to compare distributions when you have a categorical grouping variable and a continuous outcome variable. The levels of the categorical variables form the groups in your data, and the researchers measure the continuous variable. These graphs are often precursors to hypothesis tests, such as 2-sample t-tests and ANOVA.
Today, most people use software to create box plots, thus avoiding manual arithmetic and reducing errors. A box plot is based on what is known as the five-number summary, which is the minimum, 25 th percentile, . highlighting that the data are skewed and that the data are not from a normal distribution. Box plots highlight outliers.Based on your original qq-plot, it appears to me that the tails of your distribution may be too short--at least relative to the normal distribution. (This is based on my interpretation that the data values are on the Y axis "Ordered Values" and the theoretical quantiles are on the X axis.)In past articles, I showed you how to create a density chart and a box plot with jitter to visualize data distribution. Guess what? there are additional compelling methods to display data distribution. In this article, I will focus on how to combine the density chart together with the jitter chart to illustrate data distribution.
Yes it is possible. The thing is that the color depends on the distribution of data in the box plot and not in another dimension, the dimension can condition the color of the outliers. To change the color of the boxes you should edit the reference line in the graph (bottom axis > Edit Reference Line). Maybe this can help. $\begingroup$ It's worth flagging that J.W. Tukey in his Exploratory data analysis (Reading, MA: Addison-Wesley, 1977) included a dot plot of Rayleigh's data, which led to the discovery of argon, as a bimodal pattern for which box plots are useless and another display, in Tukey's case a dot plot, is needed to see the structure.
A box plot is a type of plot that displays the five number summary of a dataset, which includes:. The minimum value; The first quartile; The median value; The third quartile; The maximum value; A typical box plot looks like this: Within a box plot: The first quartile represents the 25th percentile of all values in the dataset.; The median represents the 50th percentile of . Copy all of the cell values as well as the cells with the Average label.; Click on the chart, then select the Paste button on the ribbon’s Home tab.; Click Paste Special.; Select “New Series“, “Values in Rows,” and “Series Names in First Column” in the Paste Special dialog box, then click OK. The average series shows as a Stacked Column. describes the box plots as good old Tukey box-and-whisker plot rules (e.g., whiskers extend up to 1.5X mid-band spread). . what you need to know is an image of a boxplot and the interpretation . Creating a box plot in Google Sheets is an easy way to visualize the distribution of your data. With just a few simple steps, you can make a box plot in Google Sheets to compare datasets and identify outliers. In this .
A box plot is a type of plot that displays the five number summary of a dataset, which includes:. The minimum value; The first quartile (the 25th percentile) The median value; The third quartile (the 75th percentile) The .He called his statistic Altman's Z-score, now a widely used score in finance. Based on the name of the statistic, which statistical distribution would you guess this came from? a. Normal distribution b. Poisson distribution c. Standardized normal distribution d. Uniform distribution
Just wanted to add to this brilliant answer, if you want to plot multiple boxplots after using a for loop to append multiple stats to a list e.g. (before loop: final_data = list(), within but end of loop: final_data.append(stats)) to then plot them all on one figure, remove the [] around the stats dictionary in this answer. Probably a simple . Cumulative Frequency Diagram from Group Data: https://www.youtube.com/watch?v=Y-U2NlNSaks&list=PLJ-ma5dJyAqoyNvthGAx53QQ2jevRpoSP&index=21Box and Whisker Plo. In descriptive statistics, a box plot or boxplot (also known as a box and whisker plot) is a type of chart often used in explanatory data analysis. Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots are graphical summaries of the distribution of a numerical variable, based on five key statistics: the minimum, the first quartile, the median, the third quartile, and the maximum.
The reference situation is a symmetric distribution in which the averages of paired quantiles all equal the median, so a symmetric distribution plots as a straight line. Slight and marked asymmetry are both easy to spot, as is (e.g.) approximate symmetry in the middle and marked exceptions in one or both tails. $\endgroup$ I'm trying to plot box plots with normal distribution of the underlying data next to the plots in a vertical format like this: . Now we create a little data frame of normal distributions based on the parameters taken from each group: df <- do.call(rbind, mapply( function(d, n) { y <- seq(min(d), max(d), length.out = 1000) data.frame(x = n - 5 .
Question: (a) Explain how a box plot can be used to determine whether the associated distribution of values is essentially symmetric. (6) Suppose that the histogram of the given income distribution is positively skewed. What does this fact imply about the relationship between the mean and median of this distribution? Explain your reasoning. 1. Introduction to Box Plots. Box Plots are graphical representations that display the distribution of data based on a five-number summary. These plots are particularly useful for comparing . $\begingroup$ So let me just summarise what I understood: For fitted vs residuals I want to make sure that the values are close together for each IV. The fact that only 1 point is left out from each spread indicates that the variability is ok. Regarding the box plot, we are looking at the size of the box.
Harder than our other 304 stainless steel, these thin sheets offer better wear resistance for use as a wrap, liner, or cover.
how to guess distribution based on box plots|box and whisker plot calculator